Fibonacci sequence : Deret Fibonacci, Misteri Angka Ilahi Yang Sangat Menakjubkan
Angka Tuhan, Sebenarnya itu hanya istilah saya saja untuk menyebut suatu “angka misteri” yang banyak ditemukan pada kejadian-kejadian di alam ini. Angka ini sejatinya telah banyak diteliti oleh peneliti luar negeri, mereka umumnya menyebut angka ini adalah “golden ratio” atau “golden number”. Angka ini ada kaitannya dengan deret Fibonacci atau Fibonacci sequence.
“Kekuatan terbesar dalam perhitungan modern terdapat pada tiga penemuan: notasi [bilangan] Arab, bilangan berbasis sepuluh dan logaritma”
Florian Cajori
Signifikansi perkembangan matematika pada abad pertengahan di Eropa seiring dengan lahirnya Leonardo dari Pisa yang lebih dikenal dengan julukan Fibonacci (artinya anak Bonaccio). Bonaccio sendiri artinya anak bodoh, tapi dia bukan orang bodoh karena jabatannya adalah seorang konsul yang wewakili Pisa. Jabatan yang dipegang ini membuat dia sering bepergian. Bersama anaknya, Leonardo, yang selalu mengikuti ke negara mana pun dia melakukan lawatan. Fibonacci menulis buku Liber Abaci setelah terinspirasi pada kunjungannya ke Bugia, suatu kota yang sedang tumbuh di Aljazair. Ketika ayahnya bertugas di sana, seorang ahli matematika Arab memperlihatkan keajaiban sistem bilangan Hindu-Arab. Sistem yang mulai dikenal setelah jaman Perang Salib. Kalkulasi yang tidak mungkin dilakukan dengan menggunakan notasi (bilangan) Romawi. Setelah Fibonacci mengamati semua kalkulasi yang dimungkinkan oleh sistem ini, dia memutuskan untuk belajar pada matematikawan Arab yang tinggal di sekitar Mediterania. Semangat belajarnya yang sangat mengebu-gebu membuat dia melakukan perjalanan ke Mesir, Syria, Yunani, Sisilia.
Mengarang buku
Tahun 1202 dia menerbitkan buku Liber Abaci dengan menggunakan – apa yang sekarang disebut dengan aljabar, dengan menggunakan numeral Hindu-Arabik. Buku ini memberi dampak besar karena muncul dunia baru dengan angka-angka yang bisa menggantikan sistem Yahudi, Yunani dan Romawi dengan angka dan huruf untuk menghitung dan kalkulasi.
Pendahuluan buku berisi dengan bagaimana menentukan jumlah digit dalam satuan numeral atau tabel penggandaan (baca: perkalian) dengan angka sepuluh, dengan angka seratus dan seterusnya. Kalkulasi dengan menggunakan seluruh angka dan pembagian, pecahan, akar, bahkan penyelesaian persamaan garis lurus (linier) dan persamaan kuadrat. Buku itu dilengkapi dengan latihan dan aplikasi sehingga menggairahkan pembacanya. Dasar pedagang, ilustrasi dalam dunia bisnis dengan angka-angka juga disajikan. Termasuk di sini adalah pembukuan bisnis (double entry), penggambaran tentang marjin keuntungan, perubahan (konversi) mata uang, konversi berat dan ukuran (kalibrasi), bahkan menyertakan penghitungan bunga. (Pada jaman itu riba, masih dilarang). Penguasa pada saat itu, Frederick, yang terpesona dengan Liber Abaci, ketika mengunjungi Pisa, memanggil Fibonacci untuk datang menghadap. Dihadapan banyak ahli dan melakukan tanya-jawab dan wawancara langsung, Fibonacci memecahkan problem aljabar dan persamaan kuadrat.
Problem kelinci
Pertemuan dengan Frederick dan pertanyaan-pertanyaan yang diajukan oleh ahli-ahli tersebut, dibukukan dan diterbitkan tidak lama kemudian. Tahun 1225 dia mengeluarkan buku Liber Quadrotorum (buku tentang Kuadrat) yang dipersembahkannya untuk Sang raja. Dalam buku itu tercantum problem yang mampu mengusik “akal sehat” matematikawan yaitu tentang problem kelinci beranak-pinak Pertanyaan sederhana tapi diperlukan kejelian berpikir.
“Berapa pasang kelinci yang akan beranak-pinak selama satu tahun. Diawali oleh sepasang kelinci, apabila setiap bulan sepasang anak kelinci menjadi produktif pada bulan kedua”
- Akhir bulan kedua, mereka kawin dan kelinci betina I melahirkan sepasang anak kelinci beda jenis kelamin.
- Akhir bulan kedua, kelinci betina melahirkan sepasang anak baru, sehingga ada 2 pasang kelinci.
- Akhir bulan ketiga, kelinci betina I melahirkan pasangan kelinci kedua, sehingga ada 3 pasang kelinci.
- Akhir bulan keempat, kelinci betina I melahirkan sepasang anak baru dan kelinci betina II melahirkan sepasang anak kelinci, sehingga ada 5 pasang kelinci.
Akan diperoleh jawaban: 55 pasang kelinci. Bagaimana bila proses itu terus berlangsung seratus tahun? Hasilnya (contek saja): 354.224.848.179.261.915.075.
Apakah ada cara cepat untuk menghitungnya? Di sini Fibonacci memberikan rumus bilangan yang kemudian dikenal dengan nama deret Fibonacci.
Deret Fibonacci
Orang Kristen menolak angka nol; namun pedagang dalam melakukan transaksi membutuhkan angka nol. Alasan yang dipakai oleh Fibonacci adalah nol sebagai batas. Apabila diperoleh hasil negatif berarti kerugian. Orang yang mengenalkan angka nol ini ke dunia Barat adalah Leonardo dari Pisa. Meskipun ayahnya seorang Konsul sekaligus pedagang, profesi Fibonacci – tidak mau menjadi konsul, adalah seorang pedagang. Anak muda – yang lebih dikenal dengan nama Fibonacci – belajar matematika dari orang-orang Islam dan menjadi matematikawan piawai dengan cara belajar sendiri. Menemukan deret bilangan yang diberi nama seperti namanya.
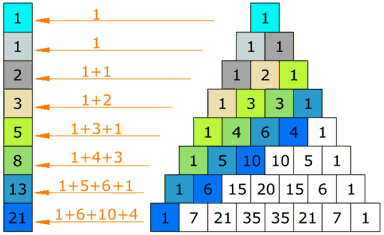
Deret Fibbonacci yaitu: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 …
Pola deret di atas terbentuk dari susunan bilangan berurutan (dari kecil makin besar) yaitu merupakan penjumlahan dua bilangan sebelumnya. Angka 3, urutan keempat, adalah hasil penjumlahan 1 (urutan 2) + 2 (urutan 3); angka 5 urutan kelima, adalah hasil penjumlahan 2 (urutan 3) + 3 (urutan 4); angka 8 urutan keenam, adalah hasil penjumlahan 3 (urutan 4) + 5 (urutan 5) dan seterusnya. Deret di atas mampu menjawab problem kelinci beranak-pinak, alur bunga lily, pola dan jumlah mata nanas, jumlah kelopak dan alur spiral bunga jenis-jenis tertentu. Lewat deret Fibonacci ini dapat diketahui diketahui urutan atau alur yang akurat pada alam. Ukuran ruangan binatang berkulit lunak (moluska) yang berbentuk spiral, nautilus *; jumlah searah jarum jam atau berlawanan jarum jam ‘mata‘ nanas, jumlah kelopak bunga matahari dan ada 2 alur spiral (ke kanan 34 dan ke kiri 55) sesuai dengan deret Fibonacci.
Kaitan dengan nisbah emas
Nisbah emas sudak dikenal sejak jaman Pythagoras. Disebutkan bahwa alam tampaknya diatur oleh nisbah emas. “Kesaktian” nisbah ini mendasari arsitektur bangunan jaman dahulu, khususnya di Yunani. Bentangan pilar dan tinggi Panthenon merupakan perbandingan hasil nisbah emas.
Perhatikan hasil pembagian bilangan-bilangan pada deret Fibonacci di bawah ini.
1/1; 2/1; 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; 144/89…
Pola apa yang terjadi? Bilangan hasil pembagian menunjukkan sesuatu yang istimewa sehingga disebut dengan seksi emas (golden section). Nama ini mirip dengan nisbah emas. Memang ada hubungan erat antara seksi emas dan nisbah emas seperti dapat dilihat pada tabel dan gambar di bawah ini.
Deret 1 2 3 5 8 13 21 34 55 89 144
Pembagi 1 1 2 3 5 8 13 21 34 55 89
Hasil 1 2 1,5 1,66 1,6 1,625 1,615 1,619 1,617 1,618 1,618
Barangkali kenyataan ini mampu menjawab pertanyaan mengapa deret Fibonacci mendekati nisbah emas.
Ambil contoh dua bilangan: a, b, a+b (deret Fibonacci) dan b/a (nisbah emas) kemudian diperbandingkan
b/a ≈ (a+b)/b
b/a (nisbah emas) ≈ a/b + 1 (seksi emas)
Substitusikan nisbah emas dengan notasi Φ (phi) untuk persamaan di atas.
Φ = 1/Φ + 1 (kalikan ruas kiri dan kanan dengan F) hasil:
Φ² – Φ – 1 = 0
Φ = (1+ √5)/2 ≈ 1,618
Revolusi Fibonacci
Topik dalam buku Liber abaci juga menjelaskan proses aritmatik, termasuk cara mencari akar bilangan. Problem-problem dalam buku ini lebih ditekankan untuk penggunaan dalam transaksi perdagangan, sistem pecahan untuk menghitung pertukaran mata uang. Fibonacci menggunakan pecahan – biasa, bilangan berbasis enam puluh (seksadesimal) dan satuan – bukan bilangan berbasis sepuluh (desimal). Penulisan 5/12 28 biasa kita kenal sebagai 28 5/12. Dia juga menempatkan bilangan pecahan berupa komponen-kompenen yang belum dijumlah. Penulisan 115/6, sebagai contoh, ditulis dengan 1/3 ½ 11. Tidak puas dengan kebingungan ini pecahan satuan ternyata lebih membingungkan. Pecahan 98/100, sebagai contoh, dipecah menjadi 1/100 1/50 1/5 ¼ ½, dan 99/100 ditulis dengan 1/25 1/5 ¼ ½.
Masih belum jelas, terlebih notasi:
1 6 2
2 9 10
yang berarti:
1 + 6 + 2
2.9.10 9.10 10
Barangkali sangatlah mengherankan, pedagang jaman kuno sudah mampu mengoperasikan sistem bilangan sebegitu rumitnya. Penulisan pecahan di atas diadopsi dari sistem bilangan Byzantium.
* Jangan salah mengartikan dengan Nautilus yang menjadi nama kapal selam pada buku karangan Jules Verne “20.000 Leagues Under the Sea”
Sumbangsih
Mengenalkan angka nol dan menghitung pola-pola alam tidak lazim sekaligus memberi dasar pada pengenalan aljabar ke dunia Barat adalah sumbangsih terbesar Fibonacci. Mampu menciptakan deret Fibonacci yang memberi jawaban atau alasan tentang pola alam seperti yang dijabarkan dalam nisbah emas. Adopsi angka nol untuk penulisan dan melakukan perhitungan di Eropa – mengubah sistem bilangan Romawi yang tidak efisien – dengan sistem bilangan Hindu-Arabik ini kelak sangat mempengaruhi perkembangan matematika di benua Eropa. Sistim bilangan pecahan Fibonacci yang rumit, kemudian disederhanakan untuk kepentingan perdagangan. Perhatikanlah perubahan harga saham-saham yang diperdagangkan di Wall Street menggunakan sistem pecahan.
Angka fibonacci
Angka fibonacci adalah urutan angka (deret angka) yang disusun oleh Leoanardo Fibonacci pada tahun 1175 – 1245 M. Bilangan fibonacci dikenal juga dengan sebutan the golden number of human life.
Percaya atau tidak, menurut kepercayaan para ilmuwan di zaman dahulu kala, angka Fibonacci adalah salah satu bukti adanya Tuhan (inilah salah satu alasan saya memberi judul angka Tuhan). Wah kok bisa?
Apa sih sebenarnya bilangan Fibonacci itu? Bilangan Fibonacci adalah urutan angka yang diperoleh dari penjumlahan dua angka didepannya, misalnya seperti ini :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, dst
Penjelasan : Misal Angka 5, diperoleh dari penjumlahan 2 angka didepannya yaitu 2+3.
Mungkin Anda kemudian bertanya, lalu apa kaitannya angka2 itu dengan bukti adanya Tuhan?
Bilangan Fibonacci ini menunjukkan beberapa fakta aneh, tetapi sebelumnya kita perlu mengetahui terlebih dahulu mengenai angka Phi? Apa itu angka Phi?
Pasti Anda tahu, angka Phi adalah angka 1.618. Apa hubungannya dengan fibonacci? Phi merupakan hasil pembagian angka dalam deret Fibonacci dengan angka didepannya.
Misalnya 3:2, 34:21, 89:55.
Semakin besar angka Fibonacci yang dilibatkan dalam pembagian, hasilnya akan semakin mendekati 1.618.
Misteri Angka Ilahi
“Sesungguhnya Allah menciptakan segala sesuatu menurut ukuran” (Qur’an, 54:49)Jika demikian, tampaknya kemunculan deret Fibonacci dalam berbagai objek di alam bisa menjadi salah satu buktinya. Deret Fibonacci muncul dalam karya Leonardo Fibonacci (dikenal pula sebagai Leonardo Pisano), Liber Abaci, di tahun 1202. Dalam karya itu dikemukakan sebuah kasus mengenai sepasang kelinci—jantan dan betina. Pasangan kelinci ini tidak dapat bereproduksi sampai setidaknya berusia sebulan, jadi pada bulan pertama hanya ada sepasang kelinci. Pada akhir bulan kedua, sang betina melahirkan sepasang kelinci, juga jantan dan betina, sehingga kini ada 2 pasang kelinci. Pada akhir bulan ketiga, kelinci betina awal melahirkan sepasang lagi kelinci sehingga kini ada 3 pasang kelinci.
Berikut beberapa fakta yang ditemukan di alam ini.
Pada akhir bulan keempat, kelinci betina awal kembali melahirkan sepasang kelinci, sementara kelinci betina yang lahir dua bulan lalu melahirkan pasangan kelinci pertamanya sehingga kini ada 5 pasang kelinci, demikian seterusnya. Jika tidak ada kelinci yang mati maka jumlah pasangan kelinci pada tiap awal bulan akan mengikuti pola berikut : 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,…Inilah yang disebut deret atau angka Fibonacci. Masing-masing angka dalam deret ini merupakan hasil penjumlahan dua angka sebelumnya, misalnya angka 21 muncul dari 8+13; 34 dari 13+21, dan seterusnya.
Jika salah satu angka dalam deret itu (mulai dari angka 5) dibagi dengan angka sebelumnya akan menghasilkan angka yang berdekatan. Angka hasil bagi ini akan tetap setelah suku ke-13 (angka 233) yaitu 1,618. Jadi 233/144=1,618; 377/233=1,618;610/377=1,618, dan seterusnya. Angka 1,618 inilah yang disebut Rasio Emas, Angka Emas, Bagian Emas, atau Proporsi Ilahi.
Sekilas, angka-angka di atas itu tak berarti apa-apa kecuali menjelaskan masalah kelinci beranak, namun kemudian angka-angka ini menjadi bahan pertanyaan dan menggugah rasa ingin tahu para ilmuwan selama berabad-abad. Mengapa banyak objek di alam memiliki pola deret Fibonacci?
Tanaman dan hewan
Tanaman tentu tak tahu-menahu tentang angka Fibonacci, tetapi banyak tanaman tumbuh dengan mengikuti pola Fibonacci. Beberapa tanaman menampakkan deret Fibonacci pada titik tumbuhnya, tempat tiga cabang terbentuk atau terpisah. Satu batang pohon tumbuh sampai membentuk sebuah cabang, menghasilkan 2 titik tumbuh. Batang pohon utama kemudian membentuk cabang lainnya, menghasilkan 3 titik tumbuh. Kemudian batang pohon dan cabang pertama menghasilkan 2 lagi titik tumbuh sehingga menjadi 5.
Susunan daun bunga beberapa bunga juga memiliki angka Fibonacci seperti 3 daun bunga pada bunga bakung dan iris; 5 pada buttercup, mawar liar, larkspur, dan columbine; 8 pada delphiniums; 13 pada marigold, ragwort, dan cineraria; 21 pada aster, black-eyed susan, dan chicory; 34 pada pyrethrum; dan 34 atau 55 pada daisy.
Di bagian tengah bunga matahari, biji-bijinya tersusun membentuk pilinan (spiral) yang membelok ke kiri dan kanan. Jika dihitung, maka jumlah masing-masing pilinan ini adalah dua angka Fibonacci berurutan, umumnya 21 dan 34, 34 dan 55, 55 dan 89, atau 89 dan 144. Hal yangs sama terjadi pada pilinan buah pohon cemara, nenas, dan blumkol.
Mengapa pola seperti itu muncul? Apakah kebetulan atau memiliki tujuan? Dalam kasus susunan daun tanaman, ternyata pertumbuhan yang mengikuti pola deret Fibonacci adalah cara terefisien untuk tumbuh. Dengan pola demikian daun-daun memiliki ruang maksimum dan menerima paparan cahaya yang maksimum.
Pola Fibonacci pada binatang bisa ditemukan pada lebah madu. Koloni lebah madu terdiri dari satu ratu, beberapa lebah jantan dan banyak lebah pekerja. Lebah betina (ratu dan pekerja) semuanya memiliki dua orang tua, ratu dan seekor lebah jantan. Sementara lebah jantan menetas dari telur-telur yang tak dibuahi, artinya mereka hanya punya satu orang tua. Dengan demikian silsilah seekor lebah jantan mengikuti pola Fibonacci yaitu 1 orangtua, 2 eyang, 3 buyut, dan seterusnya. Pola Fibonacci juga bisa ditemukan pada pilinan rumah siput.
Pada manusia
Bercerminlah, dan Anda akan menemukan angka Fibonacci pada tubuh Anda. Anda punya 1 hidung, 2 mata dan 2 tangan yang masing-masing memiliki 5 jari yang terbagi menjadi 3 ruas.
Fisiologi indera-indera manusia seperti pendengaran, penglihatan, perabaan, pembauan, dan reseptor rasa nyeri juga memiliki struktur Fibonacci.
Setiap siklus penuh struktur double helix molekul DNA memiliki ukuran panjang 34 angstrom dan lebar 21 angstrom, dua angka Fibonacci yang berurutan yang jika dibagi akan menghasilkan angka 1,619… yang mendekati Rasio Emas, 1,618.
Rasio Emas juga bisa ditemukan pada rasio (perbandingan) antara panjang lengan bawah dengan tangan; rasio antara panjang dan lebar wajah; rasio antara jarak bibir ke titik pertemuan alis dengan panjang hidung; rasio antara panjang mulut dengan lebar hidung; rasio antara jarak bahu ke puncak kepala dengan panjang kepala; Rasio antara jarak pusar ke lutut dengan jarak lutut ke ujung kaki; dan rasio antara jarak ujung jari ke siku dengan jarak pergelangan tangan ke siku.
Tak ketinggalan, objek kecil seperti struktur kristal salju hingga objek besar seperti struktur galaksi juga memiliki Rasio Emas.
Rasio emas dan keindahan
Mengapa suatu karya seni terlihat indah? Mengapa wajah seorang perempuan terlihat cantik? Ini adalah sesuatu yang bersifat relatif, namun bagi para ilmuwan dan seniman, keindahan muncul dari proporsi yang mengandung angka Rasio Emas.
Penelitian-penelitian pada para model menunjukkan bahwa wajah mereka dipenuhi Rasio Emas. Jessica Simpson, penyanyi pop dan aktris terkenal Amerika, memiliki wajah yang menarik karena wajahnya secara geometris cocok dengan Rasio Emas. Agar gigi tampak indah pun harus memiliki proporsi Rasio Emas sehingga dokter gigi harus memerhatikan hal ini.
Sejak zaman dahulu para seniman Yunani menciptakan karya mereka berdasar pada Rasio Emas, misalnya Parthenon. Leonardo da Vinci melukis wajah Mona Lisa secara sempurna pas dengan Rasio Emas. Mozart membagi sejumlah sonatanya menjadi dua bagian yang panjangnya mencerminkan Rasio Emas. Begitu pula dalam karya komposer Hungaria, Bela Bartok, dan arsitek Prancis, Le Corbusier.
Apakah bentuk proporsi Rasio Emas benar-benar menimbulkan persepsi keindahan pada manusia, masih menjadi perdebatan di antara para ahli psikologi. Sebagian kalangan percaya secara genetik, manusia terprogram untuk mengenali bahwa Rasio Emas membangkitkan rasa senang. Sebagian lagi bahkan menganggap rasio ini bersifat mistis dan Ilahiah.
1. Jumlah Daun pada Bunga (petals)
Mungkin sebagian besar tidak terlalu memperhatikan jumlah daun pada sebuah bunga. Dan bila diamati, ternyata jumlah daun pada bunga itu menganut deret fibonacci. contohnya:
- jumlah daun bunga 3 : bunga lili, iris
- jumlah daun bunga 5 : buttercup (sejenis bunga mangkok)
- jumlah daun bunga 13 : ragwort, corn marigold, cineraria,
- jumlah daun bunga 21 : aster, black-eyed susan, chicory
- jumlah daun bunga 34 : plantain, pyrethrum
- jumlah daun bunga 55,89 : michaelmas daisies, the asteraceae family
Amati beberapa gambar berikut
Pola Bunga
Pola bunga juga menunjukkan adanya pola fibonacci ini, misalnya pada bunga matahari.
Dari titik tengah menuju ke lingkaran yang lebih luar, polanya mengikuti deret fibonacci.



Kaktus Fibonacci
Tubuh Manusia
- Tangan

Bila Anda ukur panjang jari Anda, kemudian Anda bandingkan dengan panjang lekuk jari, maka akan ketemu 1.618.
- Coba bagi tinggi badan Anda dengan jarak pusar ke telapak kaki, maka hasilnya adalah 1.618.
- Bandingkan panjang dari pundak ke ujung jari dengan panjang siku ke ujung jari, maka hasilnya adalah 1.618.
- Bandingkan panjang dari pinggang ke kaki dengan panjang lutut ke kaki, maka hasilnya adalah 1.618
- Semua perbandingan ukuran tubuh manusia adalah 1.618. benarkah? silahkan membuktikannya.
Fakta-Fakta Lain
- jumlah lebah betina pasti lebih banyak dari jantan bukan? Kalau dibandingkan antara jumlah lebah betina dengan jumlah lebah jantan, maka hasilnya adalah 1.618
Kerang laut, kerang laut memiliki cangkang keras yang berbentuk spiral. kalau dibandingkan antara panjang garis spiral paling depan dengan berikutnya, maka hasilnya adalah 1.618
- Daun, tangkai, serangga, dan semua yang berbentuk spiral, bila dibandingkan antara panjang spiral terakhir dengan sebelumnya, maka hasilnya akan selalu 1.618.
- Kabarnya, Stradivarius, pencipta bola, juga menggunakan angka ini dalam peletakan lubang di bola.5. Parthenon
Bangunan yang diarsiteki oleh Phidias ini juga menggunakan perbandingan yang berdasarkan angka Phi. 1.618.Perkembangbiakan sepasang kelinci - Menurut, sebuah penelitian yang dilakukan, sepasang Kelinci berkembang biak dengan pola deret angka Fibonacci ini.
Kemenangan Obama dan deret Angka Fibonacci
Topik ini hanyalah sebuah tambahan saja. Ada sebuah penelitian yang dipublikasikan pada bulan Juni 2008, pada saat itu masih dalam tahap kampanye calon Presiden Obama dan MacCain, yang mana penelitian tersebut mengemukakan dan tepatnya mungkin meramalkan bahwa Obama akan menjadi Presiden Amerika yang ke-44.
Penelitian ini didasarkan pada kejadian-kejadian politik di Amerika yang ada kaitannya dengan kehidupan politik orang kulit hitam di Amerika (African-Americans). Pada penelitian itu disebutkan bahwa berdasarkan deret tahun kejadian politik di Amerika, maka Obama memiliki peluang yang besar untuk menjadi Presiden Amerika.
Angka Fibonacci pada Trading
Jika anda tanyakan kata fibonacci pada ahli matematika, sebagian besar dari mereka mungkin akan menjawab deret hitung. Ya fibonacci memang lebih banyak dikenal dari deret hitung yang diciptakannya. Namun jika anda tanyakan pada trader atau investor, jawaban mereka mungkin sangat berlainan dari deret hitung. Kebanyakan dari mereka mungkin akan menjawab fibonacci sebagai salah satu teknik analisa pergerakan harga. Khususnya mengenai support, resistance, dan retracement.
Leonardo Fibonacci merupakan ahli matematika, lahir di Italia sekitar tahun 1170. Dia, dianggap sebagai The Greatest European Mathematician of Middle Ages”, berhasil menemukan sebuah deret hitung matematika dan termasuk sebagai orang pertama yang memperkenalkan sistem angka Hindu – Arab.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Itulah deret hitung fibonacci yang dihasilkan dengan menjumlahkan dua angka awal untuk mendapatkan angka-angka setelahnya. Angka-angka tersebut digunakan oleh Fibonacci untuk menjelaskan pertumbuhan ideal dari populasi kelinci. Dari deret hitung ini juga dihasilkan rasio-rasio yang banyak dikenal dengan sebutan golden ratio. Namun kita tidak akan membahas lebih lanjut mengenai hal tersebut, pembahasan lebih lanjut akan berfokus pada teori dan aplikasi metode analisa dengan Fibonacci ini.
Dari sekian banyak jenis analisa dari metode Fibonacci, terdapat empat jenis yang memiliki popularitas tinggi yaitu arc, fan, retracement, dan time zone.
Fibonacci Arc
Jika diterjemahkan ke dalam bahasa Indonesia, arc berarti busur atau lengkungan. Dan memang bentuk dari arc menyerupai busur. Fibonacci Arc didapatkan dengan menarik garis virtual dari dua titik ekstrim yang terjadi. Harga terendah dengan harga tertinggi, lalu tiga garis arc digambarkan dengan nilai tengah berada di garis arc kedua, ketiga garis arc tersebut melibatkan rasio Fibonacci di level 38.2%,50.0%, dan 61.8%.
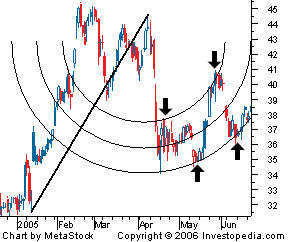
Pada gambar 1 terlihat bahwa di titik 1, 2, dan 3 memberikan indikasi adanya level support dan resistance ketika harga sedang bergerak naik dan turun.
Interpretasi dari arc melibatkan antisipasi terhadap level support dan resistance ketika harga mendekati arc. Teknik umum yang digunakan adalah menggunakan kombinasi dari Fibonacci Arc dan garis Fibonacci Fan dan mendapatkan support dan resistance dari titik pertemuan kedua garis tersebut. Namun titik pertemuan yang representatif dan signifikan untuk dijadikan dasar analisa antara Fibonacci Arc dengan Fibonacci Fan tidak akan terlalu sering dapat ditemukan. Hal ini dapat disebabkan oleh skala grafik yang ada. Support dan resistance yang dihasilkan dari titik pertemuan antara Fibonacci Arc dengan Fibonacci fan merupakan sebuah support dan resistance yang kuat.

Gambar 2
Yang perlu diperhatikan adalah skala yang digunakan dalam grafik, karena crossing harga dari Arc sangat bervariasi tergantung dari skala grafik yang digunakan.
Fibonacci Fan
Garis Fibonacci Fan didapatkan dengan menggambarkan garis trend virtual yang menghubungkan harga terendah dengan harga tertinggi ataupun sebaliknya. Fibbonacci fan menghasilkan tiga buah garis trend dengan level Fibonacci berada di 38.2%, 50%, dan 61.8%.

Gambar 3
Pada gambar 3 terlihat bahwa garis Fibonacci Fan dapat memberikan level-level support dan resistance ketika harga berusaha untuk melewati atau melakukan penetrasi.
Penggunaan garis fibbonacci fan ini hampir sama dengan penggunaan arc, namun menjadi lebih sederhana karena bentuknya merupakan garis trend. Penetrasi terhadap garis ini merupakan kunci analisa sebagai level support dan resistance. Selain itu, karena bentuknya merupakan garis trend, perubahan arah trend kadangkala dapat terlihat dari penembusan garis Fibbonacci Fan ini.
Fibonacci Retracement
Banyak analis dan trader yang memiliki gaya dan karakteristik analisa berdasarkan pergerakan koreksi atau rebound dari harga. Mereka akan berusaha untuk mencari harga tertinggi atau terendah lalu mengambil posisi setelahnya. Pandangan bahwa harga akan berbalik arah (retrace) dari pergerakan awal setelah terjadi pergerakan yang cepat memang bukan hal yang asing lagi dan untuk mendapatkan level-level tujuan pergerakan harga setelah pergerakan yang cepat dengan sifat support maupun resistance, Fibonacci Retracement dianggap sebagai salah satu yang terbaik.
Untuk mendapatkan Fibonacci Retracement, yang perlu dilakukan adalah menarik sebuah garis trend virtual antara harga terendah dengan harga tertinggi, begitu juga sebaliknya, lalu dihasilkan level-level support dan resistance dari rasio-rasio Fibonacci.
Support dan resistance di gambarkan dengan bentuk garis horizontal yang mewakili level Fibonacci dari 0.0%, 23.6%, 38.2%, 50%, 61.8%, 100%, 161.8%, 261.8%, 423.6%. Mungkin tidak semua level tersebut akan tampak dalam grafik karena memiliki nilai yang berjarak sangat jauh.
Gambar 4
Dalam Gambar 4 terlihat bahwa setiap rasio fibonacci atau garis horisontal fibonacci retracement kemungkinan akan menjadi level-level support resistance dari pergerakan harga.
Jika harga berhasil melewati salah satu garis horisontal, maka harga kemungkinan akan menuju garis horisontal selanjutnya dan jika harga tidak berhasil melewati sebuah garis horisontal maka harga kemungkinan akan kembali menuju garis horisontal sebelumnya. Sebagai contoh, pada

gambar 4, garis horisontal dengan rasio 50%, sedang dicoba oleh harga untuk dilewati (titik 2), namun harga tidak berhasil melewati, maka harga akan kembali bergerak menuju garis horisontal sebelumnya (rasio 38.2%) dan seterusnya.
Setelah adanya pergerakan harga yang cepat, harga memiliki kecenderungan untuk bergerak berbalik arah (retrace) dari pergerakan cepat sebelumnya. Ketika terjadi retrace harga, support dan resistance biasanya muncul di atau dekat dari level Fibonacci Retracement.
Fibonacci Time Zone
Fibonacci Time Zones merupakan sebuah seri garis vertikal. Garis-garis vertikal ini memiliki jarak sesuai dengan interval fibbonacci yaitu 1, 2, 3, 5, 8, 13, 21, 34, dan seterusnya.
Fibonacci Times Zones ini digunakan untuk melihat apakah terdapat pergerakan harga yang signifikan disekitar garis-garis vertikal tersebut.
Coba perhatikan gambar 5, dalam gambar tersebut terlihat bahwa terdapat pergerakan harga yang cukup signifikan ketika harga mendekati dan melewati garis-garis vertikal dari fibonacci time zone.
Metode analisa dengan menggunakan fibbonacci memang tidak ditujukan untuk menghasilkan sinyal beli dan jual ataupun timing masuk dan keluar pasar, namun metode fibonacci sangat berguna untuk menentukan area support dan resistance. Banyak analis menggunakan fibbonacci digabungkan dengan metode analisis lainnya seperti Elliott Wave untuk menghasilkan gambaran perpanjangan pergerakan retrace dan gelombang harga lainnya.















No comments:
Post a Comment